原文链接: How diffusion models work: the math from scratch 作者: Sergios Karagiannakos, Nikolas Adaloglou
扩散模型(Diffusion Models)是一类全新的先进生成模型,能够生成多样化的高分辨率图像。在 OpenAI、Nvidia 和 Google 成功训练大规模模型之后,它们引起了广泛关注。基于扩散模型的架构示例包括 GLIDE、DALLE-2、Imagen 以及完全开源的 Stable Diffusion。
但是它们背后的主要原理是什么?
在这篇博文中,我们将从基本原理出发,深入探讨。目前已经有许多不同的基于扩散的架构。我们将重点关注最著名的一种,即由 Sohl-Dickstein 等人发起,随后由 Ho 等人(2020)提出的去噪扩散概率模型(DDPM,Denoising Diffusion Probabilistic Models)。其他方法如 Stable Diffusion 和基于分数的模型(score-based models)也将进行简要讨论。
扩散模型与以往所有的生成方法有着根本的不同。直观地说,它们旨在将图像生成过程(采样)分解为许多小的“去噪”步骤。
这背后的直觉是,模型可以在这些小步骤中修正自己,并逐渐产生一个好的样本。在某种程度上,这种优化表征的想法已经在 AlphaFold 等模型中使用过。但是,没有任何东西是零成本的。这种迭代过程使得它们的采样速度很慢,至少与 GAN 相比是这样。
扩散过程(Diffusion Process)
扩散模型的基本思想相当简单。它们接收输入图像 并通过一系列 步逐渐向其中添加高斯噪声。我们将此称为前向过程(Forward Process)。值得注意的是,这与神经网络的前向传播无关。如果你愿意,这一部分对于生成我们神经网络的目标(应用了 步噪声后的图像)是必要的。
之后,通过逆转加噪过程,训练一个神经网络来恢复原始数据。通过能够模拟逆向过程,我们可以生成新数据。这就是所谓的反向扩散过程(Reverse Diffusion Process),或者一般称为生成模型的采样过程。
具体如何实现?让我们深入数学细节,使其清晰明了。
前向扩散(Forward Diffusion)
扩散模型可以看作是潜变量模型(Latent Variable Models)。潜变量意味着我们指的是一个隐藏的连续特征空间。从这个角度看,它们可能看起来类似于变分自编码器(VAEs)。
在实践中,它们是使用 步的马尔可夫链(Markov Chain)来公式化的。这里,马尔可夫链意味着每一步只依赖于前一步,这是一个温和的假设。重要的是,与基于流的模型(flow-based models)不同,我们不局限于使用特定类型的神经网络。
给定一个从真实数据分布 采样的数据点 (),我们可以通过添加噪声定义一个前向扩散过程。具体来说,在马尔可夫链的每一步,我们向 添加方差为 的高斯噪声,产生一个新的潜变量 ,其分布为 。这个扩散过程可以公式化如下:
图1:前向扩散过程。图片修改自 Ho et al. 2020
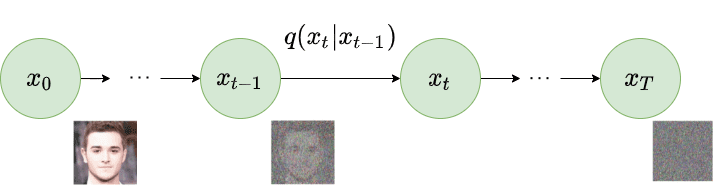
由于我们处于多维场景中, 是单位矩阵,表明每个维度具有相同的标准差 。注意 仍然是一个正态分布,由均值 和方差 定义,其中 且 。 总是方差的对角矩阵(这里是 )。
因此,我们可以以一种易于处理的方式,从输入数据 闭式地(closed form)得到 。在数学上,这是后验概率,定义为:
符号 在 中表示我们需要从时间步 到 重复应用 。这也称为轨迹(trajectory)。
到目前为止一切顺利?并不尽然!对于时间步 ,我们需要应用 500 次才能采样 。难道我们真的不能做得更好吗?
**重参数化技巧(Reparameterization trick)**为此提供了一个神奇的补救措施。
重参数化技巧:任意时间步的闭式采样
如果我们定义 ,,其中 ,我们可以使用重参数化技巧以递归方式证明:
注意:由于所有时间步都具有相同的高斯噪声,我们从现在开始只使用符号 。
因此,为了生成样本 ,我们可以使用以下分布:
由于 是一个超参数,我们可以预先计算所有时间步的 和 。这意味着我们可以在任意时间步 采样噪声并一次性得到 。因此,我们可以在任意时间步采样我们的潜变量 。这将是我们稍后计算易于处理的目标损失 的目标。
方差调度(Variance Schedule)
方差参数 可以固定为一个常数,也可以在 个时间步中选择作为一个调度(schedule)。实际上,人们可以定义一个方差调度,它可以是线性的、二次的、余弦的等。最初的 DDPM 作者使用了一个从 增加到 的线性调度。Nichol et al. 2021 表明,采用余弦调度效果更好。
图2:分别来自线性(上)和余弦(下)调度的潜变量样本。来源:Nichol & Dhariwal 2021

反向扩散(Reverse Diffusion)
当 时,潜变量 几乎是一个各向同性高斯分布。因此,如果我们设法学习反向分布 ,我们就可以从 采样 ,运行反向过程并从 获取样本,从而从原始数据分布中生成一个新的数据点。
问题是我们如何对反向扩散过程进行建模。
用神经网络近似反向过程
在实际术语中,我们不知道 。它是难以处理的(intractable),因为统计估计 需要涉及数据分布的计算。
相反,我们使用参数化模型 (例如神经网络)来近似 。由于 也将是高斯的,对于足够小的 ,我们可以选择 为高斯分布,并仅参数化均值和方差:
图3:反向扩散过程。图片修改自 Ho et al. 2020
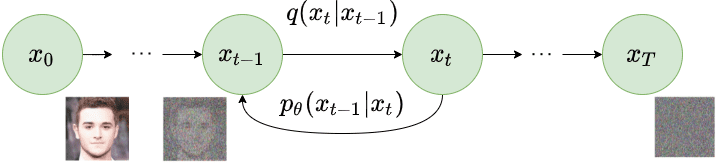
如果我们对所有时间步应用反向公式(,也称为轨迹),我们可以从 回到数据分布:
通过额外地在时间步 上调节模型,它将学会预测每个时间步的高斯参数(即均值 和协方差矩阵 )。
但是我们如何训练这样的模型?
训练扩散模型(Training diffusion models)
如果我们退一步,我们可以注意到 和 的组合与变分自编码器(VAE)非常相似。因此,我们可以通过优化训练数据的负对数似然(negative log-likelihood)来训练它。经过一系列计算(我们这里不进行分析),我们可以写出证据下界(ELBO):
让我们分析这几项:
- 可以被视为重建项(reconstruction term),类似于 VAE 的 ELBO 中的那一项。
- 显示了 与标准高斯分布有多接近。注意这一项没有任何可训练参数,因此在训练期间被忽略。
- 第三项 描述了期望的去噪步骤 与我们的近似项 之间的差异(KL 散度)。
很明显,通过 ELBO,最大化似然归结为学习去噪步骤 。
注意:尽管 是难以处理的,Sohl-Dickstein 等人展示了通过以 为条件,它变得易于处理: 。
直观地说,画家(模型)需要参考图像()来慢慢绘制(反向扩散步骤 )图像。因此,当且仅当我们有 作为参考时,我们可以向后退一小步,即从噪声生成图像。
换句话说,我们可以以噪声水平 为条件对 进行采样。由于 近似于 ,我们可以证明我们需要用网络近似均值 。
通过一些推导(省略细节),损失函数可以简化为:
这实际上告诉我们,模型不是预测分布的均值,而是预测每个时间步 的噪声 。
Ho et al. (2020) 对实际损失项进行了一些简化,因为他们忽略了一个加权项。简化版本优于完整目标。作者发现优化上述目标比优化原始 ELBO 效果更好。
此外,Ho et al. (2020) 决定保持方差固定,让网络只学习均值。后来 Nichol et al. 2021 对此进行了改进,让网络学习协方差矩阵(通过修改 ),从而取得了更好的结果。
图4:DDPM 的训练和采样算法。来源:Ho et al. 2020

架构(Architecture)
到目前为止我们还没提到的一件事是模型的架构是什么样的。请注意,模型的输入和输出应该具有相同的大小。
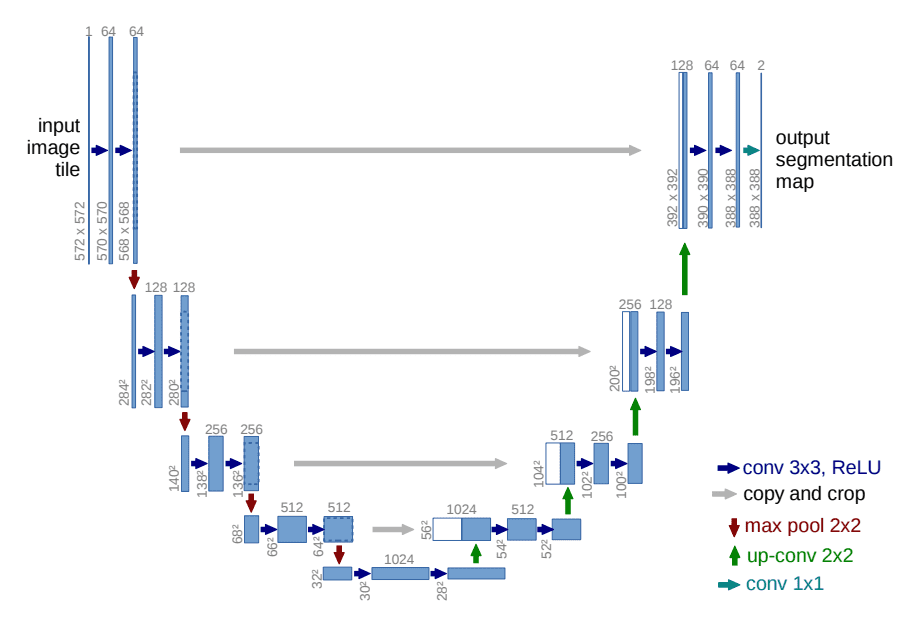
为此,Ho 等人采用了 U-Net。U-Net 是一种对称架构,其输入和输出具有相同的空间大小,并在相应特征维度的编码器和解码器块之间使用跳跃连接(skip connections)。通常,输入图像首先被下采样,然后被上采样直到达到其初始大小。
在 DDPM 的原始实现中,U-Net 由 Wide ResNet 块、Group Normalization 和 Self-Attention 块组成。
扩散时间步 通过在每个残差块中添加正弦位置嵌入(sinusoidal position embedding)来指定。
图5:U-Net 架构。来源:Ronneberger et al.
条件图像生成:引导扩散(Guided Diffusion)
图像生成的一个关键方面是调节采样过程以操纵生成的样本。这也称为引导扩散。
数学上,引导指的是用条件 (即类别标签或图像/文本嵌入)调节先验数据分布 ,产生 。
为了将扩散模型 转化为条件扩散模型,我们可以在每个扩散步骤添加调节信息 :
分类器引导(Classifier Guidance)
Sohl-Dickstein 等人以及后来的 Dhariwal 和 Nichol 表明,我们可以使用第二个模型——分类器 ——在训练期间引导扩散朝向目标类别 。为此,我们可以在噪声图像 上训练一个分类器来预测其类别 。然后我们可以使用梯度 来引导扩散过程。
其中 是引导尺度(guidance scale)。
图6:分类器引导扩散采样算法。来源:Dhariwal & Nichol 2021

无分类器引导(Classifier-Free Guidance)
Ho & Salimans 提出可以在没有第二个分类器模型的情况下实现引导。作者训练了一个条件扩散模型 和一个无条件模型 。实际上,他们使用完全相同的神经网络。在训练期间,他们随机将类别 设置为 0,以便模型同时暴露于条件和无条件设置。
这种方法避免了需要单独的分类器,并且通常能产生更好的结果。
基于分数的生成模型(Score-based Generative Models)
Song 和 Ermon 提出了一种不同类型的生成模型,似乎与扩散模型有许多相似之处。基于分数的模型利用**分数匹配(score-matching)**和 Langevin 动力学来解决生成学习。
分数匹配是指对数概率密度函数的梯度建模过程,也称为分数函数(score function)。Langevin 动力学是一个迭代过程,可以使用其分数函数从分布中提取样本。
通过使用随机微分方程(SDE),Song et al. (2021) 探索了基于分数的模型与扩散模型的联系。他们表明,扩散过程可以被建模为 SDE 的离散化形式。
图7:基于分数的生成模型与分数匹配及 Langevin 动力学。来源:Song & Ermon
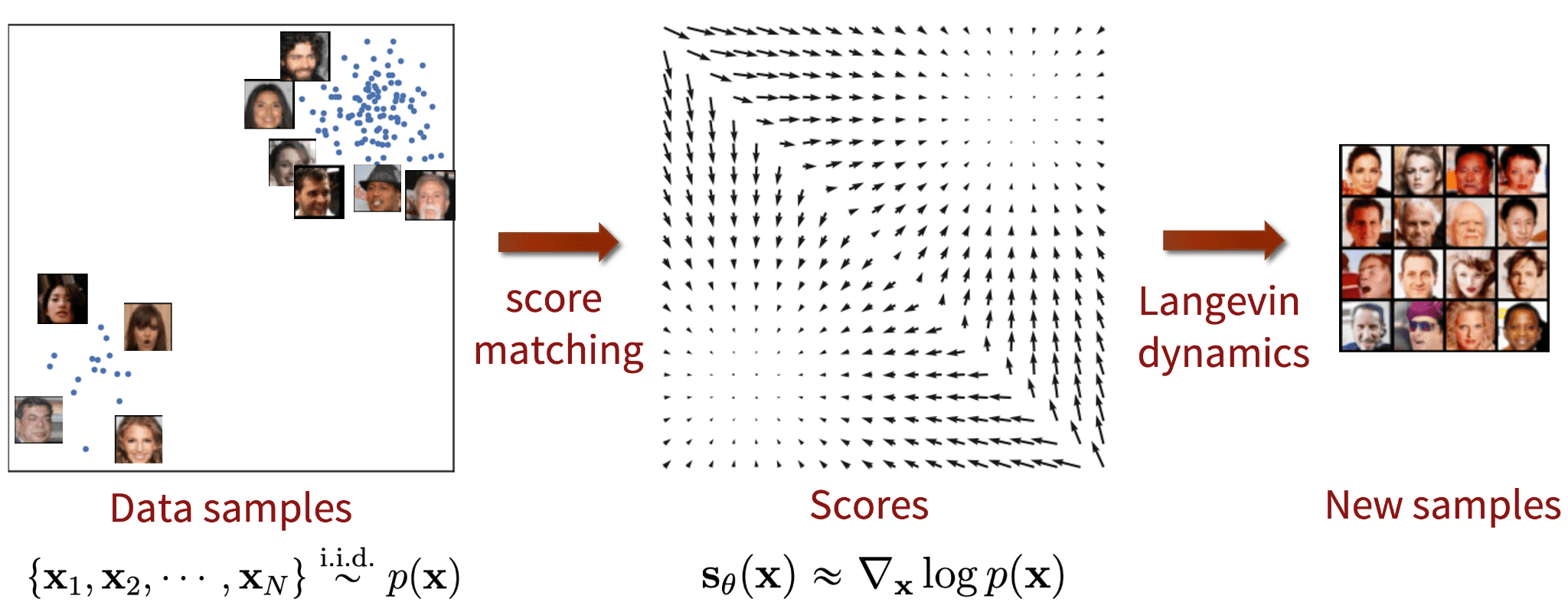
图8:通过 SDE 进行基于分数的生成建模概述。来源:Song et al. 2021




